Some More Noise

I haven't had time to post lately, but it's because I've been working on lots of stuff! Mostly water for the upcoming C6 Demo App (gonna be the best realtime ocean anyone's ever done, at least I hope) and school, but I've also added quite a bit to my Perlin Noise generator. New techniques like taking all the noise to a user-specified power, taking the real or absolute value of the raw data before I interpolate it to create the octaves, and simply inverting the noise all create extremely different variations on the cloud pattern I discussed a few weeks ago.

I think the generator is ready to be posted online...or at least will be soon, but until then, I've got a bunch of pictures to share of noise I generated, both height maps and normal maps, as well as the settings that produced them. I hope you enjoy them, because it's amazing how varied they are when you consider the simple way in which they're created. Plenty of possibilities for texture, and I have a feeling I've barely scratched the surface.

There should be more to come later on about my adventures with using Perlin Noise for textures, as well as a new technique I'm developing called "Wind Mapping" for some really neat ocean effects, but until that time, here are those pics I promised. Enjoy!

Making Some Noise

I promised a post about Perlin Noise, so I thought I'd share what I've learned so far. If you're not familiar with the topic, Perlin Noise (invented by Ken Perlin) is a method of using random numbers to generate fractal-like patterns that have any number of applications to computer graphics. My best reference to the subject (both interesting and informative!) is by an individual named (I assume) Hugo Elias. It can be found here. I used it heavily while creating my Perlin Noise generation program. In essence, multiple levels of noise (noise as in random data points, not noise as in someone else's music), with different frequencies and amplitudes, are added together to create a fractal-like pattern. Higher amplitudes are used for the lower frequencies so that the higher frequency noise (ie the more like static it appears) is barely visible. The following images should give you an idea of what I mean by high- and low-frequency noise. I apologize for the atrocious layout, but I'm pretty new to this and I'm having a hard time getting the pictures to appear where I want them!



















Some high frequency noise (note how dark it is (low amplitude)) and some lower frequency noise, This is brighter (higher amplitude) so it has a more pronounced effect on the image.
So what's the point of these pictures? Well, where it gets interesting is when you start adding them together. Check out this picture of 6 octaves of noise added together:

Looks pretty neat, doesn't it? Still not very useful, though, unless you want to make floor tiles or a neat picture to hang on your wall. The real magic happens when we individually blur each of the layers, or "octaves" of noise. So far my program only does this with linear blurring (rather than Gaussian or Bicubic that you'll see in Photoshop), but the results are still strikingly different. Check it out:










Multiple octaves of THIS....


















Create THIS!










Pretty cool, huh?



Finally, the last thing I've done with these images (so far), is used a GLSL shader to create a thresholding effect (like Photoshop's "Levels" command). Basically what the thresholding does is look at the value for a particular pixel. If that value is below the lower limit of the threshold, the pixel is turned black. If it's above the upper limit, it's turned white. If it's in between, it's set to an appropriate greyscale value. The effect is I can create sorts of image out of the same noise data. Behold!

The original image:

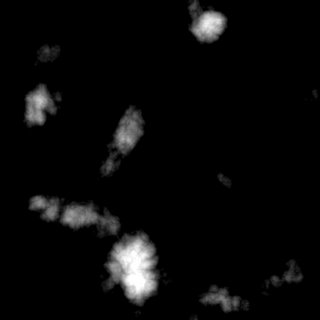
And the two thresholded versions. The one on the right could be used for clouds, whereas the one on the left could be used as a height map for Terrain.


















So there you have it. My adventures thus far with Perlin Noise. I'm going to experiment with creating animated Perlin Noise soon, and hopefully apply that to water. I'll let you know how it goes. Until next time....

[ken]

Let's Get This Started!

Okay, so I just came back from a talk by one of the greatest people I have the pleasure of knowing, Adrian Sannier. He gave a great talk, but in a nutshell, his message was this: start a blog to show off your work and your thoughts, and good things will come from it. So I'm doing just that.

So, to start off, I'm Ken. I work at the Virtual Reality Applications Center at Iowa State University as a research assistant. They're hoping to kick me out at the end of next semester, but we'll just see about that. I love programming--mainly graphics, games, and virtual reality. When I can, I combine all of those to make some amazing things. And amazing isn't a word I just throw around. For something to be amazing, it has to amaze people. Not just me, but other people around me. People who work with me and people who've been around the block a few times and people who could care less about what I do. And I'd like to think I do have some amazing things to share with the world, which is why I'm gonna stick them on here for everyone to see. So go ahead and subscribe to this blog. Tell your friends to subscribe to this blog. Because when I post things, they're gonna be the latest and greatest of what I'm doing....or they may be things I've done in the past that I think are worth showing to the world. There might also be some martial arts stuff in here too, because great stories and pictures come out of punching and kicking other people. All I know for sure is it'll be fun and interesting.


....this is kind of awkward. I've never really written a blog entry before, except my lame blog on myspace that I never update. I have to say I don't really know how I'm supposed to close an entry. I suppose I could just say come back when I post my next entry. It'll be either about Perlin noise or my killer Virtual Reality program called SkyPaint...I haven't decided which. Until next time...

[ken]
The GL Alchemist